This is Part II of a series exploring the Law Enforcement Officer Diversity dataset released by the NJ OAG. Part I is here.
The target of this post is to assemble a large combined_table with each row representing a municipal police department, containing data from the NJ OAG Use Of Force and Law Enforcement Officer Diversity datasets, plus demographic and geographic data from the US Census. The combined table will look like this:
| Field | Description | Year | Source |
|---|---|---|---|
| GEOID | US Census Geographical Identifier | US Census | |
| officer_count | Number of full-time officers | 2021 | NJ OAG Law Enforcement Officer Diversity Dataset |
| officer_mean_age | Mean age of officers | 2021 | NJ OAG Law Enforcement Officer Diversity Dataset |
| officer_r_male | Proportion of officers that are male | 2021 | NJ OAG Law Enforcement Officer Diversity Dataset |
| officer_r_white | Proportion of officers that are White | 2021 | NJ OAG Law Enforcement Officer Diversity Dataset |
| officer_r_black | Proportion of officers that are Black | 2021 | NJ OAG Law Enforcement Officer Diversity Dataset |
| officer_r_asian | Proportion of officers that are Asian | 2021 | NJ OAG Law Enforcement Officer Diversity Dataset |
| officer_r_hispanic_or_latino | Proportion of officers that are Hispanic or Latino | 2021 | NJ OAG Law Enforcement Officer Diversity Dataset |
| officer_r_race_other | Proportion of officers of other races | 2021 | NJ OAG Law Enforcement Officer Diversity Dataset |
| officer_r_two_or_more_races | Proportion of officers of two or more races | 2021 | NJ OAG Law Enforcement Officer Diversity Dataset |
| officer_r_race_na | Proportion of officers whose race is not available | 2021 | NJ OAG Law Enforcement Officer Diversity Dataset |
| population | Population | 2019 | US Census estimates |
| density | Population density | 2019 | US Census estimates |
| r_white | Proportion White (P003002 / P001001) | 2010 | US Census Decennial, SF1 |
| r_black | Proportion Black or African American (P003003 / P001001) | 2010 | US Census Decennial, SF1 |
| r_native_american | Proportion American Indian or Alaska Native (P003004 / P001001) | 2010 | US Census Decennial, SF1 |
| r_asian | Proportion Asian (P003005 / P001001) | 2010 | US Census Decennial, SF1 |
| r_pacific_islander | Proportion Native Hawaiian and Other Pacific Islander (P003006 / P001001) | 2010 | US Census Decennial, SF1 |
| r_other_races | Proportion other races (P003007 / P001001) | 2010 | US Census Decennial, SF1 |
| r_two_or_more_races | Proportion two or more races (P003008 / P001001) | 2010 | US Census Decennial, SF1 |
| r_non_hispanic_or_latino | Proportion Non-Hispanic or Latino (P004002 / P001001) | 2010 | US Census Decennial, SF1 |
| r_hispanic_or_latino | Proportion Hispanic or Latino (P004003 / P001001) | 2010 | US Census Decennial, SF1 |
| household_median_income | Household median income (B19013_001) | 2015-2019 | US Census ACS |
| shore_town |
TRUE if municipality shares a border with the Atlantic Ocean
|
2020 | US Census |
| incident_count | Number of use of force incidents | 2021 | NJ OAG Use of Force Dataset |
| partial year | Estimated portion of year that use of force incidents were reported | 2021 | NJ OAG Use of Force Dataset |
| incident_rate_est | Estimate of yearly rate of incidents of use of force | 2021 | NJ OAG Use of Force Dataset |
Packages used in this post
In this post, I’ll be using the following packages.| Package | Title | Version |
|---|---|---|
| njoagleod | NJ OAG Law Enforcement Officer Diversity data package | 1.1.3 |
| njoaguof | NJ OAG Use of Force data package | 1.4.0 |
| tidyverse | Easily Install and Load the ‘Tidyverse’ | 1.3.1 |
| lubridate | Make Dealing with Dates a Little Easier | 1.8.0 |
| scales | Scale Functions for Visualization | 1.2.0 |
| tidycensus | Load US Census Boundary and Attribute Data as ‘tidyverse’ and ‘sf’-Ready Data Frames | 1.2.2 |
| tigris | Load Census TIGER/Line Shapefiles | 1.6.1 |
| sf | Simple Features for R | 1.0-7 |
This is not a tutorial for using these packages, but all the R code used to generate the plots and tables will be included.
The OAG packages can be installed from github:
install_github("tor-gu/njoaguof")
install_github("tor-gu/njoagleod")Gathering the data
We are going to gather and combine data from several sources:
- 2021 municipal agency officer count and diversity data from
njoagleod - 2021 use of force incident counts from
njoaguof - 2019 population estimates from the US Census
- Race and ethnicity data from the 2010 US Census
- Household median income from the 2015-2019 ACS
- A “jersey shore” flag, derived from shapefiles from the US Census (see Part I)
Municipal agency diversity data
We start by getting a summary of the officer diversity data in njoagleod.
library(tidyverse)
library(njoagleod)
officer_info <- officer %>% group_by(agency_name, agency_county) %>%
summarize(
officer_count = n(),
officer_r_male = sum(officer_gender == "Male", na.rm = TRUE) / n(),
officer_mean_age = mean(officer_age, na.rm = TRUE),
officer_r_race_na = sum(is.na(officer_race) / n()),
officer_r_white = sum(officer_race == "White", na.rm = TRUE) / n(),
officer_r_black = sum(officer_race == "Black", na.rm = TRUE) / n(),
officer_r_asian = sum(officer_race == "Asian", na.rm = TRUE) / n(),
officer_r_hispanic_or_latino =
sum(officer_race == "Hispanic", na.rm = TRUE) / n(),
officer_r_race_other = 1 - sum(c_across(
officer_r_race_na:officer_r_hispanic_or_latino
)),
.groups = "drop"
) %>%
left_join(agency, by = c("agency_name", "agency_county")) %>%
filter(!is.na(municipality)) %>%
left_join(municipality, by = c("agency_county"="county", "municipality")) %>%
select(
GEOID,
officer_count,
officer_mean_age,
officer_r_male,
officer_r_white:officer_r_hispanic_or_latino,
officer_r_race_other,
officer_r_race_na
)| GEOID | officer_count | officer_mean_age | officer_r_male | officer_r_white | officer_r_black |
|---|---|---|---|---|---|
| 3402500070 | 41 | 37 | 0.95 | 0.88 | 0.02 |
| 3400100100 | 29 | 38 | 0.93 | 0.93 | 0.03 |
| 3400300700 | 15 | 43 | 0.87 | 1.00 | 0.00 |
| 3402500730 | 9 | 40 | 1.00 | 1.00 | 0.00 |
| 3402500760 | 6 | 35 | 1.00 | 1.00 | 0.00 |
| 3400301090 | 12 | 42 | 0.75 | 0.92 | 0.08 |
Note that the municipalites are identified here by US Census GEOID. We will
repeat this pattern for each of the tables, joining them together at the end
using the GEOID as the key.
Jersey Shore flag
We create a table with a shore_town flag, as in
Part I. The flag is TRUE if the municipality has a border with the Atlantic
Ocean.
library(tigris)
library(sf)
options(tigris_use_cache = TRUE)
counties <- municipality %>% pull(county) %>% unique() %>% sort()
# Get the map from tigris
nj_municipality_map <- counties %>%
map_df(~ county_subdivisions("NJ", county = ., class = "sf"))
# Get the towns that border the Atlantic Ocean
jersey_shore_water <- nj_municipality_map %>%
filter(ALAND == 0) %>%
filter(GEOID != "3401100000")
jersey_shore_indices <- st_intersects(jersey_shore_water,
nj_municipality_map) %>%
unlist() %>% unique()
# Now build a table of shore towns
municipality_shore <- nj_municipality_map %>%
as_tibble() %>%
mutate(shore_town = FALSE)
municipality_shore$shore_town[jersey_shore_indices] = TRUE
municipality_shore <- municipality_shore %>%
filter(ALAND != 0) %>%
select(GEOID, shore_town)| GEOID | shore_town |
|---|---|
| 3400107810 | TRUE |
| 3400120290 | FALSE |
| 3400129430 | FALSE |
| 3400149410 | FALSE |
| 3400160600 | FALSE |
| 3400168430 | FALSE |
Population estimates and race and ethnicity data
Next we gather the race and ethnicity data from the US Census. We are using the
tidycensus package to get the data from the 2010 decennial census.
library(tidycensus)
# Get race/enthnicity ratios (2010 / get_decennial)
municipality_race_ethnicity_ratios <- counties %>%
map_df(
~ get_decennial(
geography = "county subdivision",
state = "NJ",
county = .,
year = 2010,
output = "wide",
variables = c(
population = "P001001",
white = "P003002",
black = "P003003",
native_american = "P003004",
asian = "P003005",
pacific_islander = "P003006",
other_races = "P003007",
two_or_more_races = "P003008",
non_hispanic_or_latino = "P004002",
hispanic_or_latino = "P004003"
)
)
) %>%
filter(population != 0) %>%
# Convert totals to ratios
mutate(across(white:hispanic_or_latino, ~ .x / population)) %>%
rename_with( ~ paste0("r_", .), white:hispanic_or_latino) %>%
select(GEOID, r_white:r_hispanic_or_latino)| GEOID | r_white | r_black | r_native_american | r_asian | r_pacific_islander | r_other_races |
|---|---|---|---|---|---|---|
| 3400100100 | 0.76 | 0.10 | 0.00 | 0.08 | 0 | 0.03 |
| 3400102080 | 0.27 | 0.38 | 0.01 | 0.16 | 0 | 0.14 |
| 3400120290 | 0.70 | 0.10 | 0.00 | 0.12 | 0 | 0.05 |
| 3400108680 | 0.73 | 0.09 | 0.01 | 0.02 | 0 | 0.12 |
| 3400108710 | 0.78 | 0.13 | 0.00 | 0.01 | 0 | 0.04 |
| 3400115160 | 0.98 | 0.00 | 0.00 | 0.01 | 0 | 0.01 |
Next we gather the the population and population density from the 2019
estimates, again using the tidycensus package.
# Get population and density (2019 / get_estimates)
municipality_population <- counties %>%
map_df(
~ get_estimates(
geography = "county subdivision",
state = "NJ",
county = .,
year = 2019,
output = "wide",
product = "population"
)
) %>%
select(GEOID, population = POP, density = DENSITY)| GEOID | population | density |
|---|---|---|
| 3400108680 | 4284 | 566 |
| 3400120350 | 4052 | 373 |
| 3400129280 | 25746 | 232 |
| 3400149410 | 5856 | 104 |
| 3400100100 | 8818 | 1613 |
| 3400102080 | 37743 | 3508 |
Household median income
Next, we get figures for the household median income from the 2015-2019 ACS.
municipality_income <- counties %>%
map_df(
~ get_acs(
geography = "county subdivision",
state = "NJ",
county = .,
year = 2019,
output = "wide",
variables = c(household_median_income = "B19013_001")
)
) %>%
select(GEOID, household_median_income = household_median_incomeE) %>%
filter(!is.na(household_median_income))| GEOID | household_median_income |
|---|---|
| 3400100100 | 70393 |
| 3400160600 | 112917 |
| 3400115160 | 82500 |
| 3400149410 | 82663 |
| 3400168430 | 61366 |
| 3400143890 | 83045 |
Use of force incident counts
Finally, we gather 2021 counts of use of force incidents from the njoaguof
package. This task is somewhat complicated by the fact that we (probably) do not
have the full year of data from every municipality. The earliest incidents in
the dataset are from October 2020, but many individual agencies do not have
incidents until 2021. For example, here are all the incidents reported by the Watchung PD, from October 2020 through May 2022.
library(njoaguof)
incident %>%
filter(
agency_county == "Somerset County" &
agency_name == "Watchung PD"
) %>%
ggplot() + geom_histogram(aes(x=incident_date_1), binwidth=30) +
scale_x_date(limits=lubridate::ymd(c("2020-10-01","2022-05-31"))) +
xlab("Date") + ylab("Number of incidents") +
labs(title=str_wrap("Watchung PD use of force incidents"),
subtitle = str_wrap("Oct 2020 - May 2022"),
caption = "Source: NJ OAG")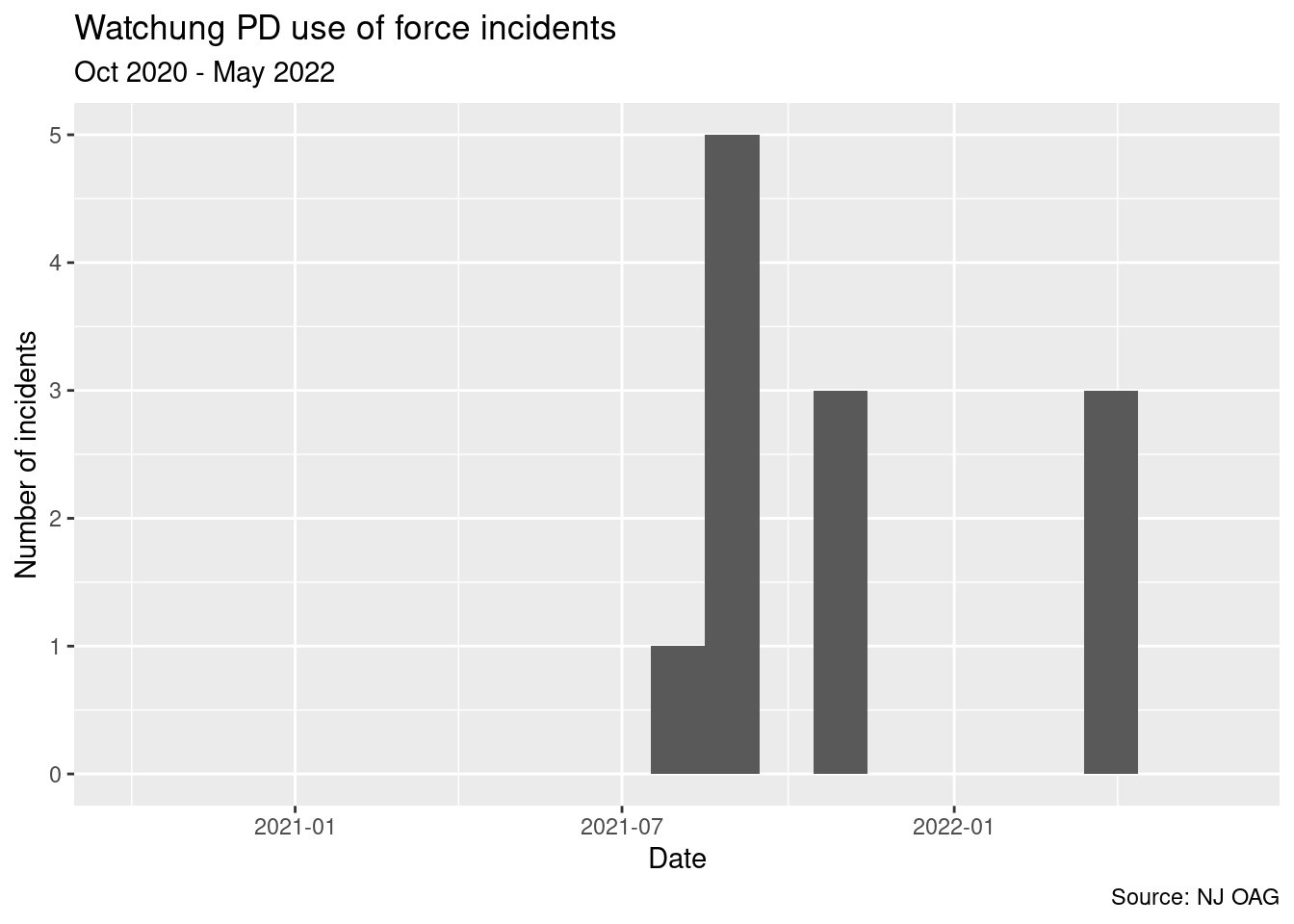
One suspects that there may have been use of force incidents between October 2020 and July 2021 that went unreported by the Watchung PD, simply because they had not yet started reporting such incidents at the time. It is not clear the earliest date at which the Watchung PD would have reported a use of force incident, but it may have been well into 2021.
For this reason, we will attempt to estimate when each department started reporting use of force incidents. We will make the simplifying assumption that for each department, the incidents represent a homogeneous Poisson process with an unknown starting point and continuing through the end of 2021. 1 For agencies which reported their first incident in 2021, we estimate the rate \(\lambda\) of incidents by looking at the period after the first incident to the end of the year: \[\lambda_{est}=n/d\] where \(n\) is the number of incidents after the first one, and \(d\) is the number of days from the first incident to the end of 2021. For a Poisson process with rate \(\lambda\), the expected value of the time until the first incident is \(e^{-\lambda}/(1-e^{-\lambda})\). Thus we estimate the start of the reporting period \(t_0\) as \[{t_0}_{est} = t_1 - e^{-\lambda_{est}}/(1-e^{-\lambda_{est}})\] where \(t_1\) is the date of the first incident. 2 Note that in order to use this estimate, there must be at least two incidents in 2021.
Let us now calculate \(\lambda_{est}\) and \({t_0}_{est}\) and the estimated proportion of the year 2021 this represents for every municipal agency who reported their first incident in 2021:
initial_incident_2021_estimates <- incident %>%
# Find the first incident and the number of incidents after
group_by(agency_county, agency_name) %>%
summarize(
first_incident = min(incident_date_1),
incidents_after_first = sum(lubridate::year(incident_date_1) == 2021) - 1,
.groups = "drop"
) %>%
filter(lubridate::year(first_incident) == 2021) %>%
mutate(
# Estimate lambda
lambda_est_period = lubridate::ymd("2022-01-01") - first_incident,
lambda_est = incidents_after_first / as.double(lambda_est_period),
# Estimate t_0
t_0_est = case_when(
incidents_after_first == 0 ~ as.Date(NA),
TRUE ~ first_incident - exp(-lambda_est) / (1 - exp(-lambda_est)),
),
# Estimate the partial year
reporting_days_est = lubridate::ymd("2022-01-01") -
pmax(t_0_est, lubridate::ymd("2021-01-01")),
partial_year = as.double(reporting_days_est) /
as.double(lubridate::ymd("2022-01-01") - lubridate::ymd("2021-01-01"))
) %>%
# Filter out non-municipal agencies
left_join(agency, by = c("agency_county", "agency_name")) %>%
filter(!is.na(municipality)) %>%
select(agency_county, municipality, lambda_est, t_0_est, partial_year)| agency_county | municipality | lambda_est | t_0_est | partial_year |
|---|---|---|---|---|
| Atlantic County | Linwood city | 0.02 | 2021-02-11 | 0.89 |
| Atlantic County | Longport borough | 0.03 | 2021-10-15 | 0.21 |
| Atlantic County | Margate City city | 0.02 | 2021-04-06 | 0.74 |
| Atlantic County | Mullica township | 0.03 | 2021-01-06 | 0.98 |
| Bergen County | Allendale borough | 0.01 | 2020-12-20 | 1.00 |
| Bergen County | Carlstadt borough | 0.02 | 2020-12-01 | 1.00 |
There are 117 municipal agencies that reported their first incident in 2021. Of these, only 13 reported a single incident in 2021; we cannot estimate the the start of the reporting period for these. Of the remainder, we reckon that we have a full year of reporting for 49 and a partial year for 55:
initial_incident_2021_estimates %>% count(partial_year< 1)## # A tibble: 3 × 2
## `partial_year < 1` n
## <lgl> <int>
## 1 FALSE 49
## 2 TRUE 55
## 3 NA 13Now we can build a table of all municipal agencies with an incident in either 2020 or 2021 and estimate the yearly rate of incidents for 2021.
- For municipalities with an incident in 2020, this rate is exactly the number of incidents in 2021.
- For municipalities that reported their first incident in 2021, the estimated
rate is the number of incidents reported 2021 divided by
partial_year.
incident_rate_2021 <- incident %>%
# Get the 2021 incident count
filter(lubridate::year(incident_date_1) <= 2021) %>%
group_by(agency_county, agency_name) %>%
summarize(incident_count = sum(lubridate::year(incident_date_1) == 2021),
.groups = "drop") %>%
# Filter out the non-municipal agencies
left_join(agency, by = c("agency_county", "agency_name")) %>%
filter(!is.na(municipality)) %>%
select(agency_county, municipality, incident_count) %>%
# Add a partial_year field, initialed to 1.0, and then update
# with the initial_incident_2021_estimates
mutate(partial_year = 1.0) %>%
rows_update(
select(
initial_incident_2021_estimates,
agency_county,
municipality,
partial_year
),
by = c("agency_county", "municipality")
) %>%
# Estimate the 2021 yearly rate
mutate(incident_rate_est = incident_count / partial_year)Finally, let’s switch to using the GEOID as the primary key.
municipality_incident_rate <- incident_rate_2021 %>%
left_join(municipality,
by = c("agency_county" = "county", "municipality")) %>%
select(GEOID, incident_count, partial_year, incident_rate_est)| GEOID | incident_count | partial_year | incident_rate_est |
|---|---|---|---|
| 3400100100 | 8 | 1 | 8 |
| 3400102080 | 119 | 1 | 119 |
| 3400107810 | 26 | 1 | 26 |
| 3400120350 | 19 | 1 | 19 |
| 3400120290 | 63 | 1 | 63 |
| 3400125560 | 83 | 1 | 83 |
Combining the tables
Before combining the tables, we have to take into account the fact that the Township of Princeton and Princeton Borough merged in 2013.
Princeton Borough and Princeton Township
The former Princeton Township
is present in the municipality_race_ethnicity_ratios table, since it is
derived from the 2010 census, but absent from the other tables. We will handle
this by updating municipality_race_ethnicity_ratios, combining the two
Princetons, weighted by their 2010 populations.
# Combine the two Princetons.
# Township: Population 16265, GEOID 3402160915
# Borough: Population 12307 GEOID 3402160900
combined_princeton <- municipality_race_ethnicity_ratios %>%
filter(GEOID %in% c("3402160900", "3402160915")) %>%
arrange(GEOID) %>%
mutate(weight = c(12307, 16265)) %>%
summarize(across(r_white:r_hispanic_or_latino,
~ sum(.x * weight) / sum(weight))) %>%
mutate(GEOID = "3402160900") %>%
relocate(GEOID)
# Update the table with new ratios for Princeton Borough
municipality_race_ethnicity_ratios <- municipality_race_ethnicity_ratios %>%
rows_update(combined_princeton, by="GEOID")US Census and Officer Diversity Race And Ethnicity Differences
Before combining the data, we should note here that the US Census and NJ OAG treat Hispanic and Latino origin differently. In the NJ OAG Law Enforcement Officer Diversity dataset, Hispanic and Latino origin is considered a race, so for officers we will have \[ r_{male} + r_{white} + \cdots + r_{non\_hispanic\_or\_latino} + \cdots + r_{two\_or\_more\_races} + r_{race\_na} = 1 \]
On the other hand, the US Census treats Hispanic and Latino origin as an ethnicity independent of race. Thus, for the general population, we will have \[ r_{white} + r_{black} + \cdots + r_{two\_or\_more\_races} = 1 \] and
\[ r_{non\_hispanic\_or\_latino} + r_{hispanic\_or\_latino} = 1 \]
The combined table
Now we can build the combined table.
combined_table <- officer_info %>%
inner_join(municipality_population, by="GEOID") %>%
inner_join(municipality_race_ethnicity_ratios, by="GEOID") %>%
inner_join(municipality_income, by="GEOID") %>%
inner_join(municipality_shore, by="GEOID") %>%
inner_join(municipality_incident_rate, by="GEOID")This table has 407 rows, of which 395 have an estimate of the incident rate. These 395 rows cover 90% of the population of New Jersey.
sum(combined_table[!is.na(combined_table$incident_rate_est),]$population) /
sum(municipality_population$population)## [1] 0.9Use of force incidents by population and officer count
Unsurprisingly, the incident rate estimate is strongly correlated with both the population and the officer count.
combined_table %>%
select(incident_rate_est,
officer_count,
population,
partial_year,
shore_town) %>%
pivot_longer(officer_count:population) %>%
ggplot(aes(x = incident_rate_est, y = value)) +
geom_point(aes(alpha = partial_year, color = shore_town)) +
geom_smooth(aes(weight = partial_year), method = "lm", se = FALSE) +
scale_x_log10() + scale_y_log10(labels=scales::comma) +
facet_wrap(facets = "name", scales = "free") +
labs(
title = str_wrap("2021 use of force incidents vs population and officer count"),
caption = "Source: US Census, NJ OAG"
) +
theme(legend.position = "bottom",
axis.title.y=element_blank())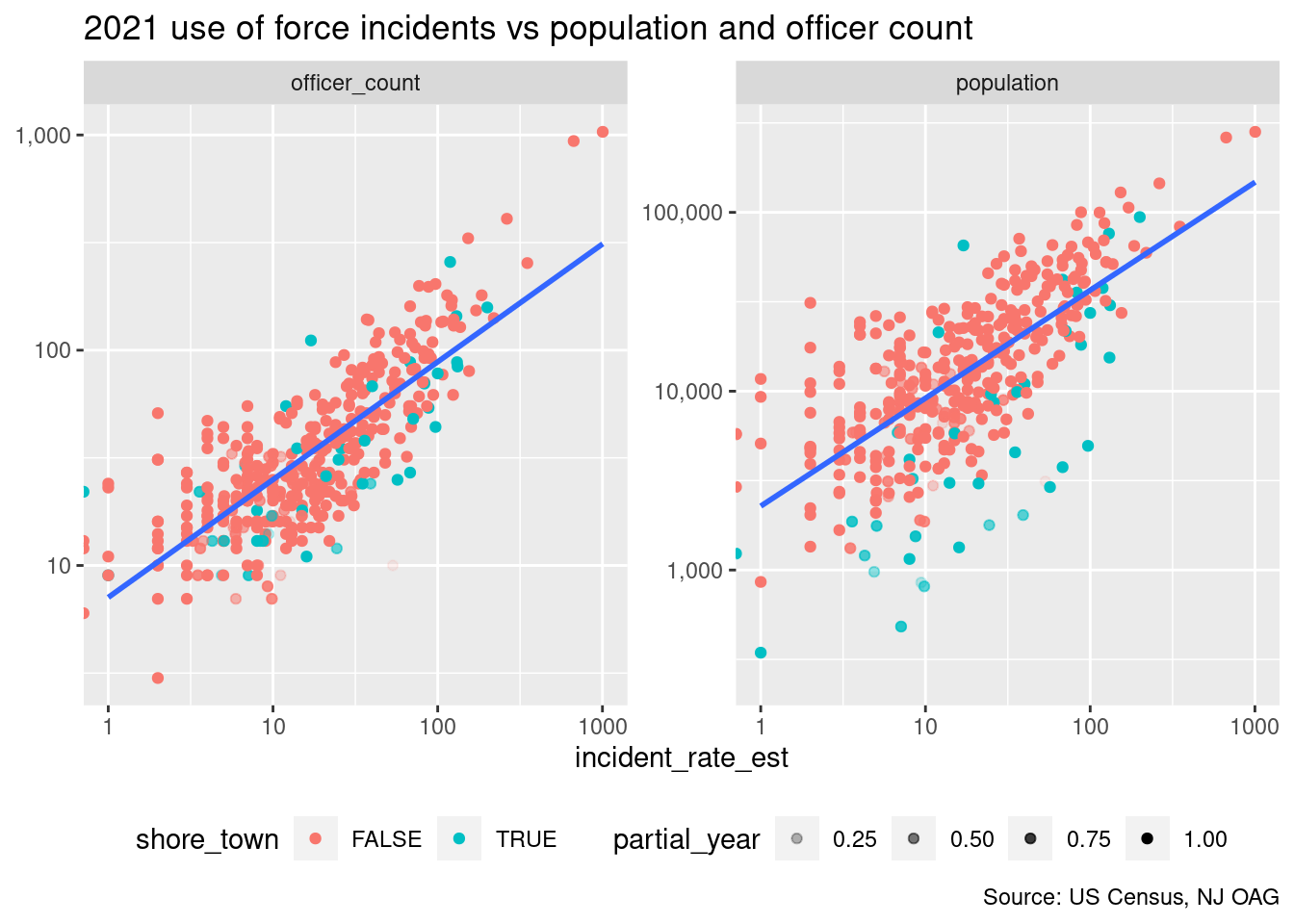
However, in a joint linear model, the officer_count is far more significant than population.
lm(incident_rate_est ~ officer_count + population,
combined_table , weights=partial_year) %>%
summary() %>%
magrittr::use_series("coefficients")## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -4.18760 1.66373 -2.5 1.2e-02
## officer_count 0.92022 0.04508 20.4 1.3e-63
## population -0.00034 0.00014 -2.5 1.3e-02As we observed in
Part I,
many of the towns on the Jersey Shore (blue dots in the chart above) have
much larger summer populations (and correspondingly larger police departments)
not reflected in the US Census population. If we exclude the shore towns, the
population becomes more significant in the joint model, though still less so
than the officer_count.
combined_table_core <- combined_table %>% filter(!shore_town)
lm(incident_rate_est ~ officer_count + population,
combined_table_core , weights=partial_year) %>%
summary() %>%
magrittr::use_series("coefficients")## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -4.45728 1.70075 -2.6 9.2e-03
## officer_count 0.98138 0.04755 20.6 1.4e-62
## population -0.00052 0.00015 -3.6 3.6e-04With this in mind, we will begin to focus on the per-officer incident rate, and try to see how variations in this rate between municipalities are explained by the other variables in our combined table.
Next
In the next post, we will use the combined_table generated in this post and begin exploring the relationship between these variables and number of use of force incidents per officer.
This is certainly a simplifying assumption, since we would expect the frequency of incidents to vary seasonally, especially for shore towns. It is also possible that some departments stopped reporting incidents some time before the end of 2021, or reported incidents sporadically. Additionally, the force incidents frequently appear in bunches because multiple officers or multiple subjects may be involved in a single event. We will not attempt account for these factors.↩︎
Note that \[1/\lambda < e^{-\lambda}/(1-e^{-\lambda}) < 1/\lambda + 1/2\] when \(\lambda > 0\), so the naive estimate \({t_0}_{est} = t_1 - d/n\) would work nearly as well.↩︎